Solution: Greek Figures
Answer: VANGELIS
Written by greenturtle3141
This puzzle is an instruction-less logic puzzle. The grid in the first row represents a sample puzzle.
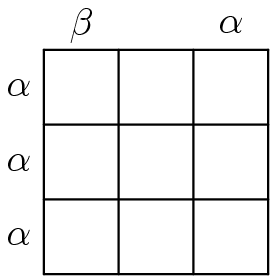
The second row shows two “bad solutions” as well as the correct solution to the sample puzzle in order to teach its rules.
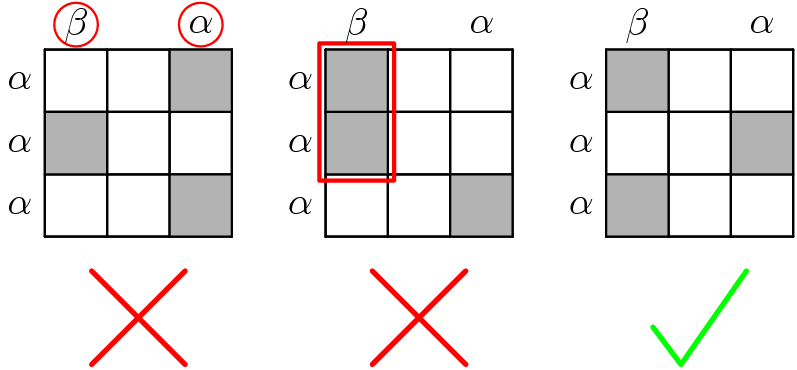
The first incorrect solution indicates that the Greek letters alpha and beta indicate how many shaded squares lie in the corresponding row/column. This hypothesis can be verified using the given correct solution. In particular, we can infer that an alpha indicates one shaded square, whereas a beta indicates two shaded squares.
The second incorrect solution simply demonstrates that two shaded squares cannot be next to each other. Although it is not clear whether or not they can be diagonally adjacent, this ambiguity can be clarified by solving the larger 5×5 puzzle.
To summarize, the rules of the logic puzzle are as follows:
- Shade some squares of the grid.
- If a row/column is labelled with an alpha, there should be exactly one shaded square in that row/column. Similarly, beta indicates two shaded squares.
- No two shaded squares may be adjacent.
Now let us solve the 5×5 puzzle at the bottom.

There is a new Greek letter that labels the bottom row: gamma. Since alpha, beta, and gamma are the first three letters of the Greek alphabet, we can infer that gamma means three shaded squares in that row. There is only one way to place those squares so that no two are adjacent:
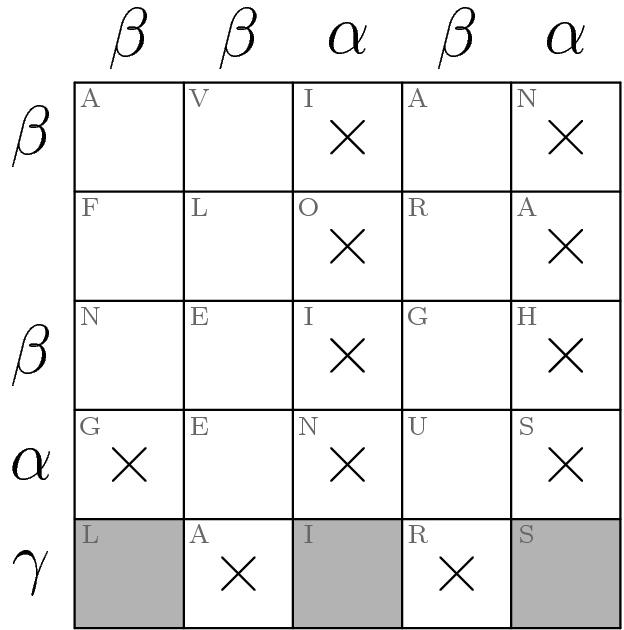
The ×'s indicate squares that we know cannot be shaded at this point.
Now notice that the second row from the top has no label. From the sample, one could infer that this means there are no shaded squares. If one desires further confirmation, note that the total number of shaded squares can be counted in two ways: by totalling the number of shaded squares in each row, or by totalling the number of shaded squares in each column. These numbers must be the same. The column labels imply that there are 2+2+1+2+1=8 shaded squares, and the row labels imply that there are 2+2+1+3=8 shaded squares among the labeled rows, which confirms that the unlabeled row has no shaded squares.
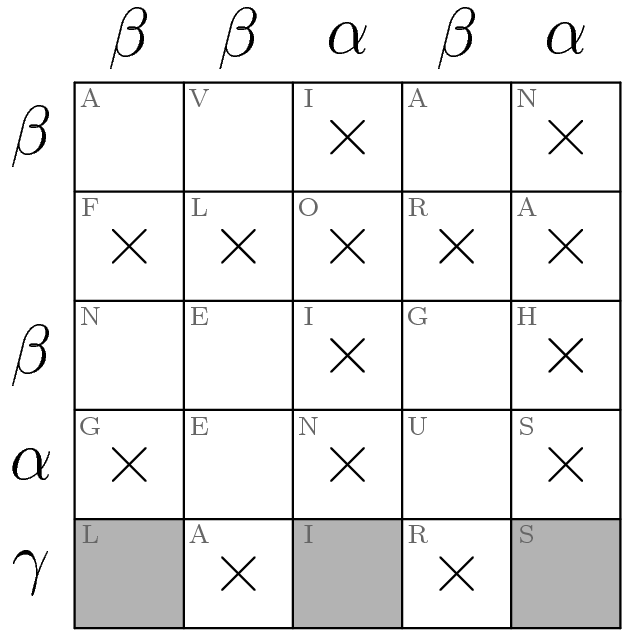
Now look at the second column from the left. If the square marked with a “V” is not shaded, then the other two squares (marked with “E”'s) must both be shaded. But this is impossible since they're adjacent, so the “V” square must be shaded. Similar reasoning may be applied to the fourth column.
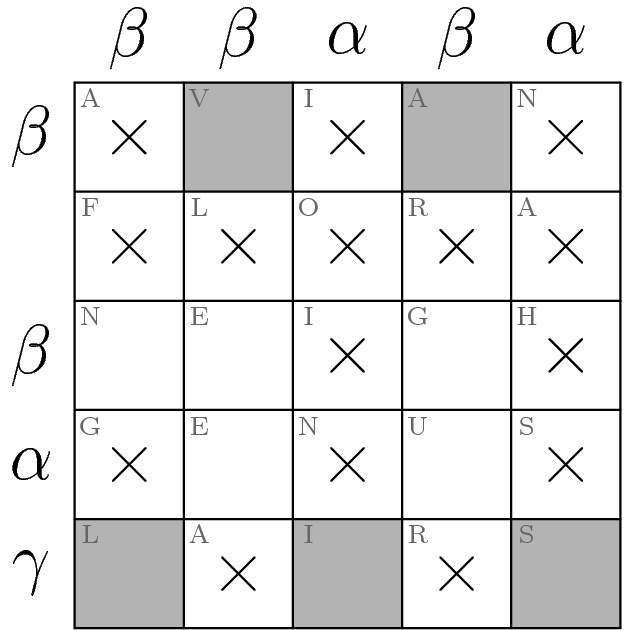
It's a straight line to the finish from here: The remaining square (with an “N”) in the first column must be shaded, which directly implies that “G” of “NEIGH” and the “E” of “GENUS” are both shaded.
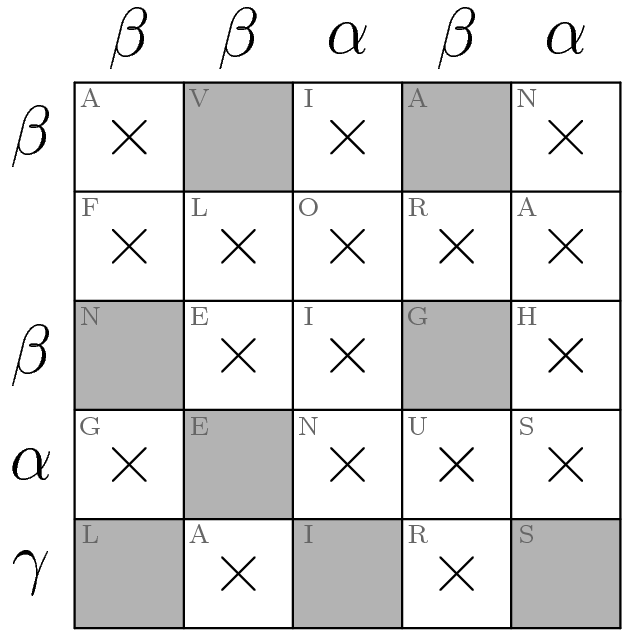
The 5×5 puzzle is now solved. To extract, read the shaded squares' letters in book order to get VANGELIS, a Greek musician (and thus a Greek Figure).